一元函数微分学的概念

导数的概念

定义

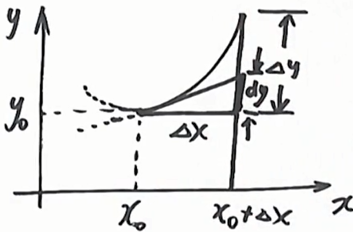
若函数y=f(x)在x0邻域内有定义，且x+∆x在邻域内，则增量∆y为

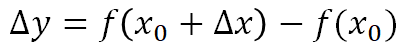
当

存在，则称f(x)在x0处可导

并称这个极限为f(x)在x0处的导数

注意：

• 增量有时候会广义化
• 可以把增量写成差的形式(两种形式)
• 等价提法
  • y=f(x)在x0处可导
  • y=f(x)在x0处导数存在
  • f’(x)=A(A为有限数)↔常数
• 单侧导数

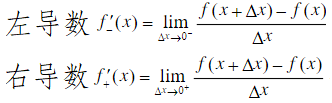
导数充要条件

导数不存在的两种情况

1.角点

y=f(x)=|x|在x=0的切线

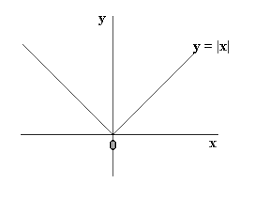
证明

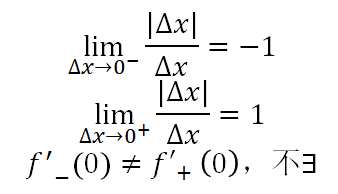
2.铅垂线

y=f(x)=x^1/3在x=0的切线

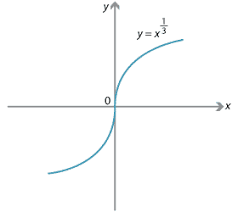
证明

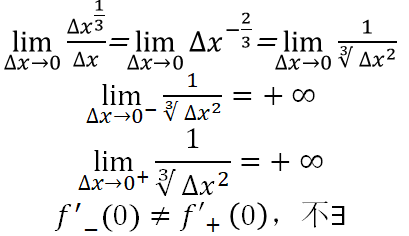
光滑不一定可导

导数的几何意义

函数y=f(x)在点x0的导数f’(x)就是y=f(x)在点(x0,y0)处的切线斜率

高阶导数

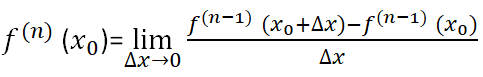
其中n≥2，x0+∆x在邻域内

微分的概念

若函数y=f(x)在x0邻域内有定义，且x+∆x在邻域内，则增量∆y为

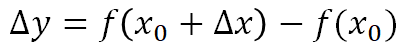
若存在一个与∆x无关的常数A，使得

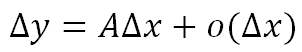
则称f(x)在x0处可微

称A∆x为f(x)在x0处的微分

A∆x被称为线性主部，o(x)称为误差，记作

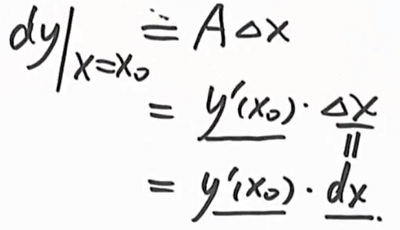
可微的判别

写增量

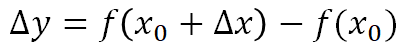
写线性增量

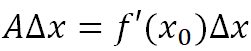
做极限

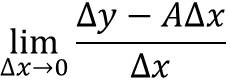
若极限等于0则f(x)在x=x0处可微，否则不可微

上面的步骤可以看出，用形式简单的量“线性增量A∆x”去代替形式复杂的量“增量∆y”，且其中误差“∆y-A∆x”是“o(∆x)”可以忽略不记，这就是微分的含义

可导必可微，可微必可导，互为充要条件

可微的几何意义